본문은 좌표계, DCM, 드론의 작용하는 힘과 모멘트, 드론의 형상에 따른 로터의 힘과 모멘트 계산, 제어할당 행렬 계산을 알아본다.
어떤 물체를 모델링함에 있어 중요해 보이는 것은 힘과 모멘트이지만 그것을 말하기 전에 어떤 위치에 물체가 있는 지를 설명해야한다.
즉, 어떤 기준(좌표계)를 기준으로 물체가 어느 곳에 위치해있는지 알아야 한다.
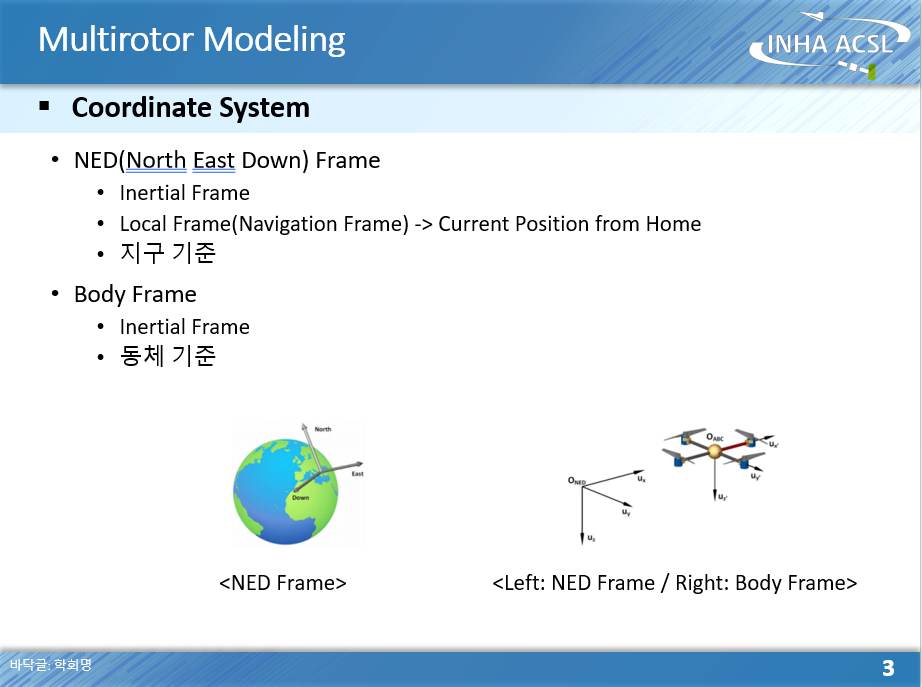
드론의 무게 중심이 Body Frame: 동체 좌표계가 되는 것이고 어떤 방향이 x축인지는 드론의 형상에 따라 달라지며 후술한다.
NED 프레임은 North-East-Down을 의미하며 지구의 표면에서 북쪽과 동쪽 그리고 지면 아래방향으로 표시하는 좌표계이다. 지구를 어떻게 모델링하는 가에 따라 정확도가 달라지기는 하며 우리가 드론을 몇 km 날릴게 아닌 이상 평평지구로 가정해서 모델링해도 상관없다. 이외에도 GCD(Great Circle Distance)라는 대원 기하학을 이용한 관성 좌표계도 있는데 전투기를 모델링하는 것은 아니므로 평평지구로만 하는 것으로 한다.
물체를 모델링하기 위해 NED와 동체 좌표계 간의 변환이 필요하다.
각 좌표계는 장점들이 있는데, NED 좌표계는 지구의 드론이 어느 위치에 그리고 어느 자세로 있는 지 관측자 입장에서 표현하는 것으로 흔히 내가 조종하는 중에 드론을 바라볼때 자세와 위치를 표현하는 좌표계라고 생각하면 된다.
동체좌표계는 드론이 기울어지면 좌표계도 기울어지는 특성을 가진다. 즉, 로터의 힘과 동체 좌표계는 같이 움직이며 로터의 힘은 모멘트에도 영향을 준다. 즉, 동체에 작용하는 힘을 쉽게 표현할 수 있는 것이 동체 좌표계이다.
그렇다면 이 좌표계 간 변환은 어떻게 하는가?
DCM(Direction Cosine Matrix)를 이용하면 된다.
먼저, 2D 좌표계 변환을 생각해보자.
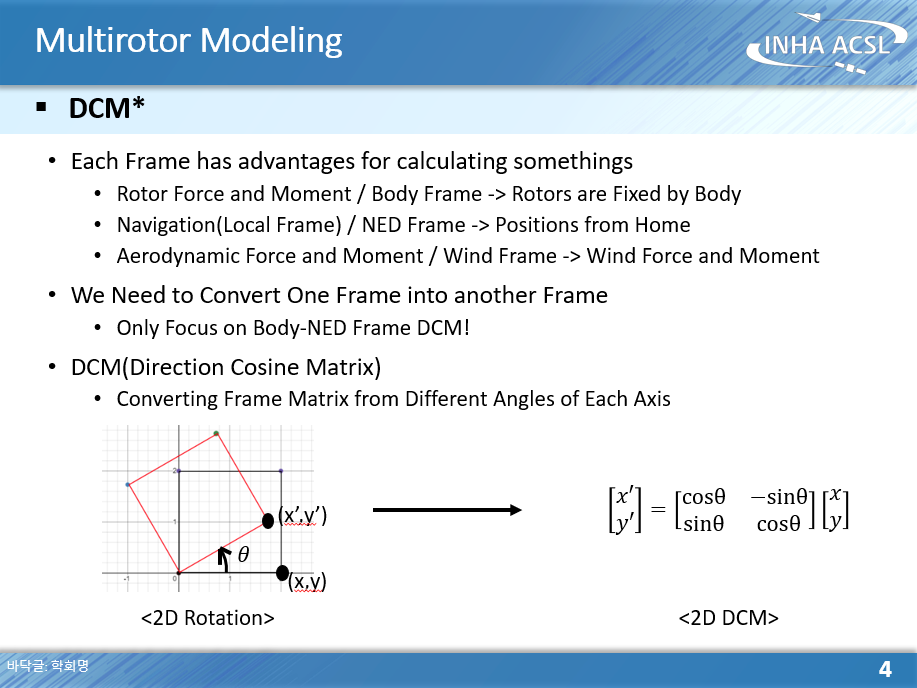
단순히 각 x,y 좌표에 얼마만큰 각도로 회전했는 지에 따라 cosine sine 함수를 곱해주는 것이 회전변환이다.
이를 3차원으로 확장시키면 다음과 같으며 우리는 3-2-1 회전만 고려할 것이다.
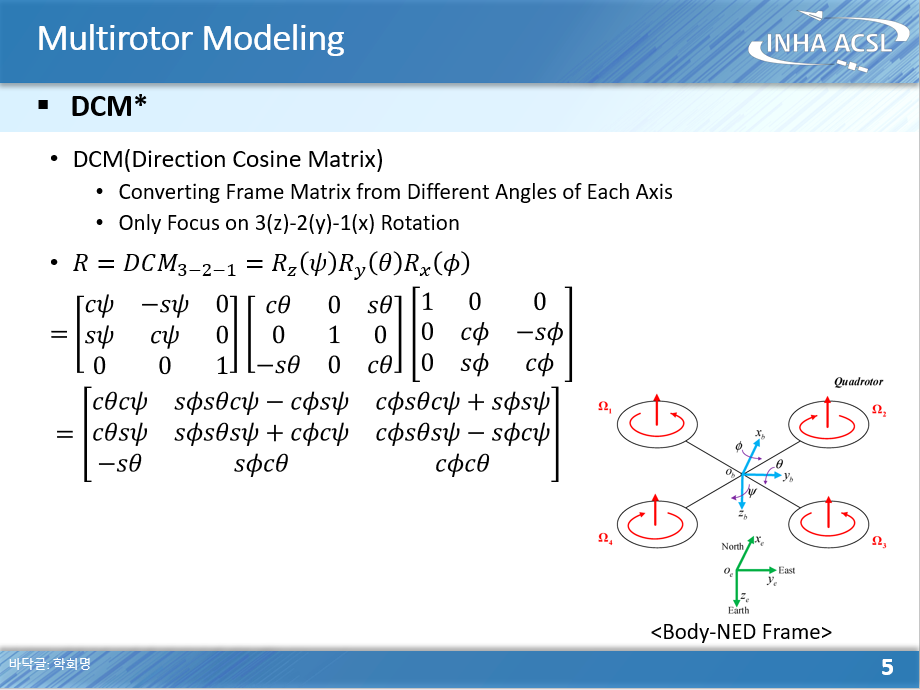
Z축 기준으로 Psi 만큼, Y축 기준으로 Theta 만큼, X축 기준으로 Phi 만큼 회전한다는 의미이며 R_z, R_y, R_x는 각각 회전행렬이라고 부른다. 회전행렬에는 재밌는 성질이 있는데 이건 알아서 찾아보도록하자
DCM을 통해 각각의 좌표계에서 표현되는 속도와 각속도를 변환하면 다음과 같다.

위에서 보면 Angular Transformation Matrix가 있는데 이건 각속도간 좌표계 변환을 의미하며 DCM이 아니다. 그래서 역행렬을 구할 때 전치를 하는 것이 아닌 무조건 역행렬로 계산해야한다.
서술한대로 동체좌표계는 동체에 작용되는 힘과 모멘트를 쉽게 표현할 수 있다고 했다.

F_b와 M_b는 외력이라고 생각하면 된다.
F_b에서 w_b X v_b라고 돼있는 부분은 원심력 힘이다.
M_b 식은 각운동량 식을 알면 알 수 있는 간단한 식이다.
I는 관성행렬이며 드론이 완벽하게 대칭이면 I_xz는 0이다. 그럴 일은 없지만
아래 fx fy fz mx my mz로 표현되는 것은 F_b와 M_b를 계산한 식을 각 축 성분으로 재표현한 것이다.
동체에 작용하는 힘과 모멘트인 F_b와 M_b를 표현해보자.
행성에서 드론을 날리므로 중력은 존재한다.
즉 동체에 작용하는 힘은 중력, 로터의 추력, 외란(바람) 정도가 있다
동체에 작용하는 모멘트는 드론의 무게 중심으로부터 로터의 추력이 발생하는 거리만큼, gyroscopic 외란(바람) 정도가 있다.

먼저 힘에 대해 얘기해보자.
중력은 지구 중심을 향하는 방향으로 작용한다. 동체가 지면과 수평이 아니면 어느 각도만큼 차이가 있을 것이다.
즉, 위에서 계산한 DCM을 통해 중력 성분을 변환해줘야한다.
다음은 로터 추력에 대한 것이며 로터가 틸트되지않는 이상 동체와 함께 기울어지므로 좌표계 변환이 필요없다.
마지막으로 외란(바람)이 있는 데 우리가 고려해야할만 한것은 바람이 불때 드론의 면적에 대한 힘이 작용되는 것 정도만 알면 될것이다.
다음은 모멘트이다.
로터의 추력과 드론의 무게중심으로부터 추력이 발생하는 로터의 거리만큼의 곱이 모멘트가 되며 이는 드론의 형상에 따라 달라지면 후술한다.
gyroscopic 효과는 피젯스피너를 돌려본 사람들한테 크게 와닿을 수 있다. 피젯스피너를 돌리면서 각도를 기울여본적이 있는가?
이때 손에 느껴지는 저항감이 바로 gyroscopic 효과이다.
피젯 스피너가 하늘 방향(z축)으로 회전하고 있을때 x축과 y축에 대해 각도 변화량(각속도)를 주면 저항감이 생기는 것 이것이 gyrosopic 효과이다.
그러나 이 효과는 로터와 프로펠러의 관성량이 매우 작으면 취급안해도 되는 미미한 모멘트를 가진다.
어쨌든 바람에 대한 모멘트 효과는 솔직히 어떻게 작용하는 지 잘 모르겠다. dryden 모델에 의한 p q r 외란을 적용하면 될거 같은데 넘어가자.
다음은 로터 동역학 모델이다.
우리가 사용할 로터 모델은 전자학 단계까지는 가지않고 대충 로터의 각속도 제곱에 추력과 토크가 비례하는 것으로 모델링할 것이다.

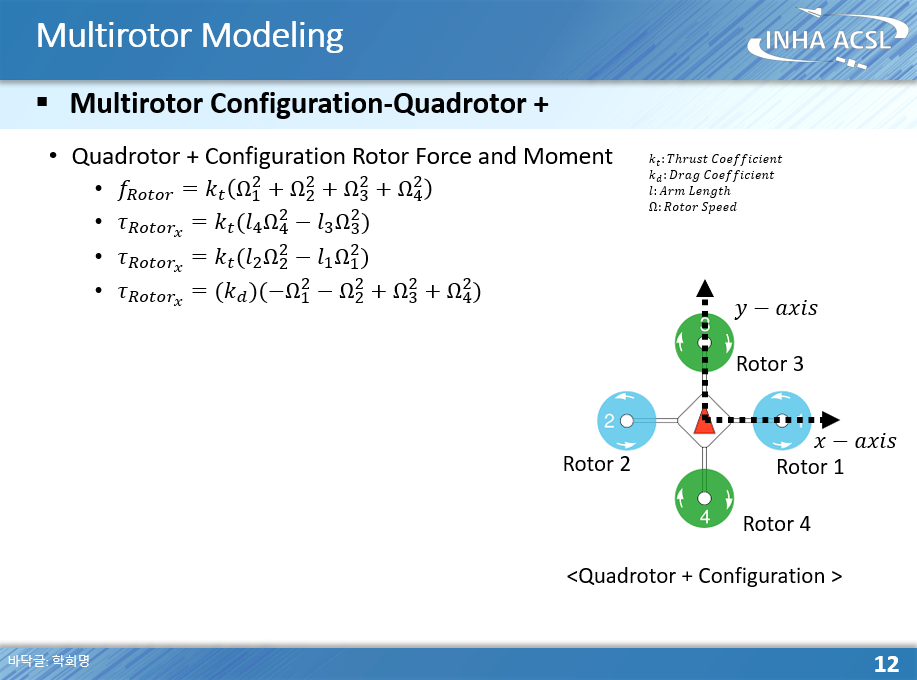
다음은 드론의 형상에 따른 x축 y축 모멘트 계산 방법이다.
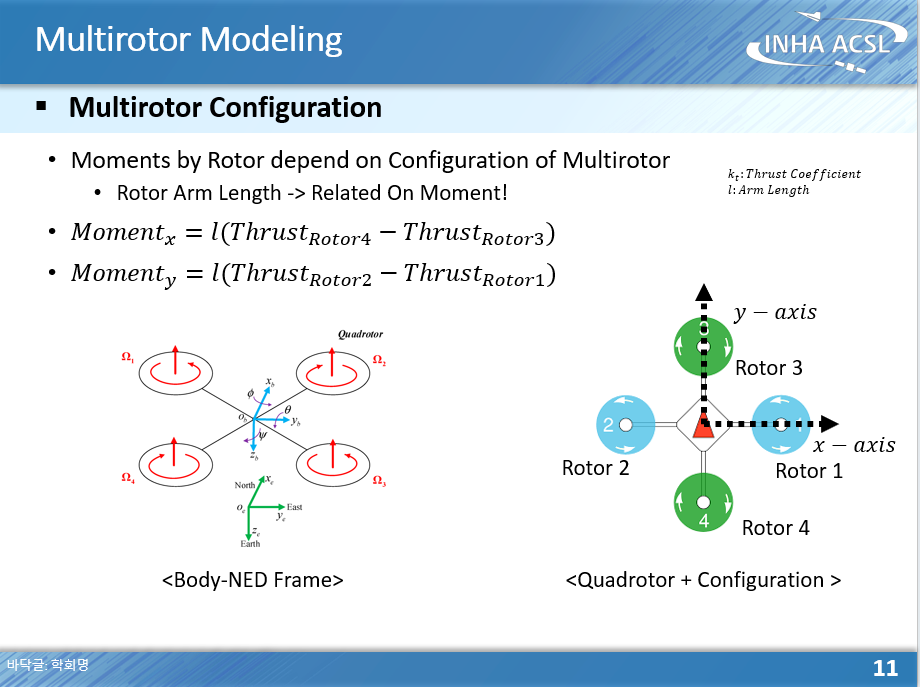
마지막으로 로터가 낼 수 있는 힘과 모멘트를 공식으로 +형상을 가지는 드론에 대해 표현한 것이다
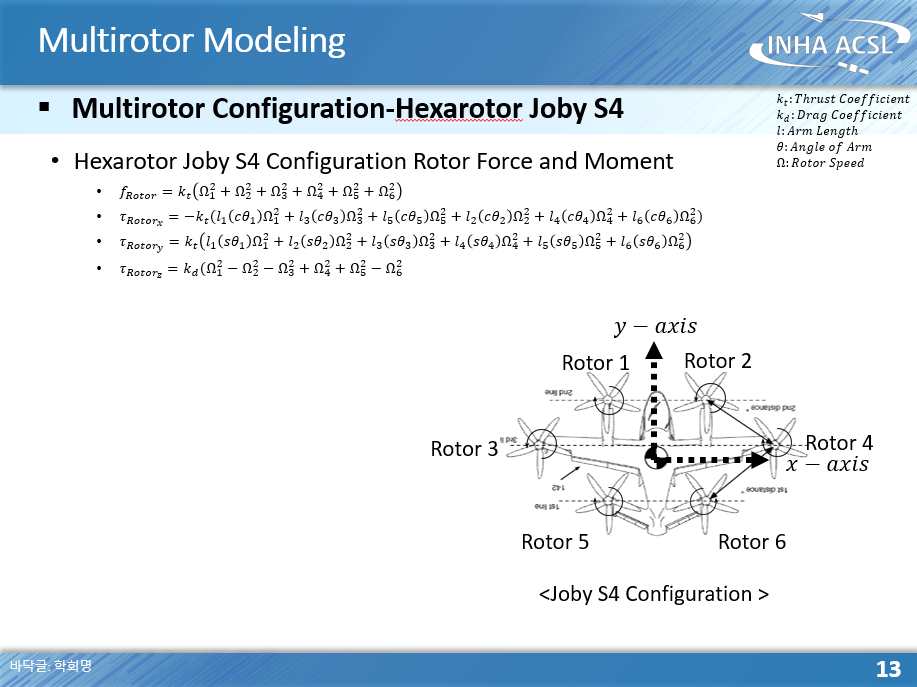
만약 Hexarotor Joby S4에 대해 나타내면 로터가 내는 힘과 모멘트는 다음과 같다.
다음은 제어할당 행렬 구하는 방법이다.
쿼드로터 형상에서 로터가 내는 힘과 모멘트에 대해서 로터의 각속도 제곱에 비례하는 것을 확인했다.
이때 우리가 드론을 제어한다고 하면 필요한 힘과 모멘트를 제어명령으로 로터의 각속도를 제어해 필요한 힘과 모멘트를 내게 될 것이다.
즉 제어명령으로 로터가 내야하는 힘과 모멘트주면 우리는 각 로터가 내야하는 각속도로 변환해서 각 로터를 제어해야 한다.
Hexarotor Joby S4에 대해 제어할당 행렬을 추출해보자.
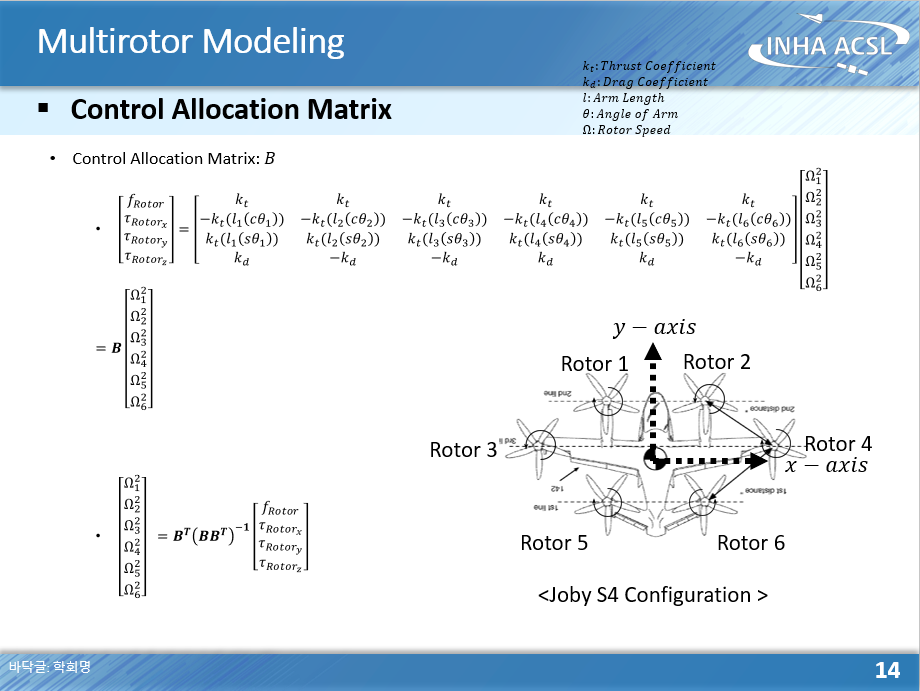
슬라이드 맨 아래 식을 보면
각속도는 = 제어할당 행렬 * (로터 힘 모멘트) 이렇게 되어있다.
여기서 B는 힘 = B * 로터 각속도 식에서 B를 의미한다.
이것을 통해 드론을 제어할 수 있게 된다.
'취미-공학' 카테고리의 다른 글
| Gazebo-ROS2 기반 시뮬레이터 만들기(0) 부제: 왜 하는가? (2) | 2023.07.08 |
|---|---|
| Sliding Mode Control & Backstepping Control 대강 알기 (1) (0) | 2022.09.01 |
| Gazebo ROS2 이용해서 SDF 모델 불러오기 (0) | 2022.05.12 |
| PX4 Gazebo Multiple Vehicle SITL with micrortps (0) | 2022.04.28 |
| px4_ros_com, px4_msgs 패키지 사용자 정의 메시지를 통해 PX4 모듈과 통신 (0) | 2022.04.16 |